讀完 Pearl Professor (Www.pearlprofessor.org). 分享的「對水」故事,我第一個反應不是「要換幾次水」,而是——
這根本是一條活生生的指數函數教材。
而且是那種學生一聽就會問:「Sir,咁原來數學真係有用㗎?」
一、為什麼這不是普通的「換水題」?
表面看來,「對水」像是一條簡單的百分比計算題:
- 每次倒走 30% 舊水
- 再補回 30% 新水
- 水量永遠維持 1 公升
但真正的關鍵是這一句:
「每一次倒走的 30%,不是原本的水,而是『剩下的舊水』。」
這一刻,問題就從線性思維,跳進了指數世界。
二、數學模型其實一句就講完
設
- 第 0 次時,舊水比例 = 1(即 100%)
- 每次操作後,舊水只剩下原來的 70%
那麼第 ( n ) 次後,舊水比例就是:
舊水比例 = 0.7n
這不是巧合,這是標準的指數衰減模型,和以下情況一模一樣:
- 放射性衰變
- 藥物在人體內的代謝
- 病毒載量下降
- 金錢「複利的反方向」
珍珠蚌,只是主角換了。
三、為什麼「換 7 次」才夠?
目標很清楚:
舊水 ≤ 10%
即0.7n ≤ 0.1
這時候,數學自然帶我們去到——對數。
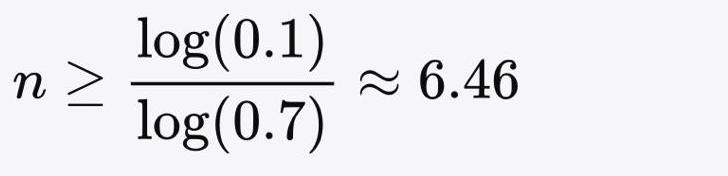
但現實世界不能「換 6.46 次水」,
所以我們要向上取整:
✅ 最少要 7 次
這一點,正正是「數學答案」與「實際操作」最漂亮的交會位。
四、為什麼這題特別適合教學生?
因為它同時做到三件中學數學最難做到的事:
1️⃣ 打破「數學只係計數」的印象
學生會發現:
原來數學不是幫你計結果
而是幫你預測過程
2️⃣ 讓指數不是抽象符號
(0.7n) 不再只是圖像上的曲線
而是:
- 每 15 分鐘
- 每一次「對水」
- 每一次珍珠蚌慢慢適應的過程
3️⃣ 自然引出更高階問題
例如:
- 如果每次只換 20% 呢?
- 想 95% 新水要幾次?
- 能否反推「每次應該換幾多水」?
學生不是被「教」,而是被「引誘」去問數學。
五、從數學角度的一句總結
「對水不是慢,而是指數地溫柔。」
珍珠蚌需要的,不是一刀切的環境轉換,
而是一條平滑、可預測、可計算的適應曲線。
而數學,正正就是那條曲線。

